Universidad
Politécnica de Madrid

21.06.18

Por José Luis Rosales y Vicente Martín,
Centro de Simulación Computacional, ETS Ingenieros Informáticos

El nuevo método determina la probabilidad de que cualquier número primo sea uno de los dos factores primos de un número dado. Después de determinar estas probabilidades, los candidatos de factores primos más probables se pueden probar primero, lo que permite identificar los factores primos mucho más rápido que antes.  

El objetivo es desarrollar una nueva teoría cuántica del problema de factorización usando un simulador cuántico,  un enfoque  que ha descubierto una propiedad sin analogía clásica en teoría de números: cada par de números primos que pueden solucionar el problema se reorganizan de un modo completamente inexplicable desde la teoría de números clásica  para formar un patrón regular: el espectro de bandas del simulador cuántico. El problema cuántico determina un algoritmo semiclásico de factorización, un nuevo método que no utiliza información proveniente  de ninguna criba clásica conocida hasta ahora.  Se trataría de una criba cuántica que usa las propiedades especiales de un sistema que simula las soluciones: un "simulador cuántico".

Cuando se codifica este sistema con el número a factorizar N=xy,  las energías del simulador exhiben una distribución de probabilidad para los pares de primos, (x,y), que, con mayor probabilidad, pueden ser los factores de N. La teoría muestra, así, no solo dónde están ubicados los números primos, sino también la probabilidad de que un primo sea un factor de un número dado. Estas conclusiones deben tener implicaciones en  criptografía porque el criptosistema RSA, basado en la dificultad  algorítmica de la factorización, ignora esta regularidad.

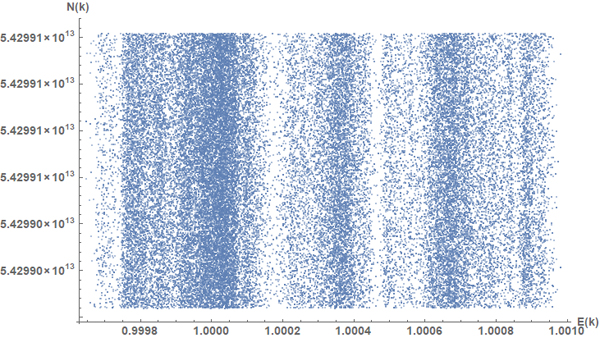
En la figura se representa el espectro cuántico de claves públicas de RSA de 46 bits (en el eje vertical). Por ejemplo N = 54299069753881= 4562219⋅11901899. Los factores posibles de estas claves se representan (en el eje horizontal) para una función aritmética E de dichos factores. En el ejemplo anterior E= 1.000883510016. Este resultado no tiene ninguna explicación desde la teoría analítica de números.  El cifrado RSA de la firma digital actualmente vigente no tiene en cuenta esta regularidad y, por lo tanto, tendremos que revisar toda la infraestructura de clave pública teniendo en cuenta la distribución cuántica.

Para entender estos resultados, intentemos poner en el contexto de la teoría de números el problema que se ha resuelto cuánticamente.

Para un factor de N dado, digamos x, lo determinante no es dar exactamente con este valor sino, más bien, calcular el orden de dicho factor dentro del conjunto de los primos, una función bien conocida en la teoría analítica de números, denominada π(x); por ejemplo π(2)=1,π(3)=2,… π(101)=26, etc. De hecho, π(x), proporciona la información óptima para resolver el problema de la factorización  ya que  no solo  permite calcular el primo x de forma unívoca a partir de esta función, sino que, también,  caracteriza que x es de hecho  un número primo. Por otra parte, conocido N, también sabemos cuántos candidatos a factorizar N existen, esto es π(√N).  Cualquier máquina, clásica o cuántica, que podamos configurar para resolver el problema debería usar como único parámetro el número π(√N) (puesto que el máximo número de divisiones que hemos de hacer para encontrar los factores de N no supera este valor). Así, por ejemplo, para resolver el problema de factorizar  el número N = 54299069753881= 4562219⋅11901899, necesitaremos como máximo π(√N)=500000  divisiones hasta hallar el factor, que  es aquel cuya división da de resto cero.  

Así pues existen otros números, próximos al N que acabamos de ver, que tienen la misma complejidad algorítmica de factorización. En nuestro ejemplo, estos son los números que cumplen π(√N')=500000.  Llamemos  Conjunto de Factorización de N a aquellos N’ que son producto de dos primos y que cumplen esta condición. Si quisiéramos calcular con una calculadora muy rápida los factores de alguno de estos N’s tendríamos que hacer exactamente, como máximo, el mismo número de divisiones en todos los casos.

Se prueba  que, para un N=xy, debe existir una máquina cuántica que calcula la probabilidad de los pares de números primos, (x,y), dentro  del Conjunto de Factorización de N. Además, las energías  de este  sistema  están directamente relacionadas con los factores dentro del conjunto [2]. Cuando el número de estados cuánticos posibles coincide con el número de elementos  del conjunto estadístico para  los factores  probables de N, la estadística cuántica reproduce la distribución de los números primos. Esta distribución es indistinguible a la mejor aproximación en teoría analítica de números, que fue calculada por Riemann. Por otro lado la universalidad de los primos (uno de los postulados de Euclides)  se obtuvo como corolario de la existencia del simulador cuántico ya que la distribución de los primos obtenida  resulta ser independiente del  N que se desee factorizar.

Los algoritmos cuánticos son mucho más eficientes que los clásicos. En el problema  que nos ocupa el número de medidas de energía  requeridas es proporcional a una potencia del logaritmo de N. Clásicamente se necesita un número operaciones  del orden de √N . Recientemente hemos  calculado  también la probabilidad relativa  de que, dado un primo, este sea un factor de N [1].

Por otro lado, el simulador es una máquina que podemos construir. Se trata de una trampa  electro-magnética (de Penning)  de dos o más iones que comparten un único estado cuántico.  

Los resultados anteriores no están de ninguna manera relacionados con los postulados de Euclides, son propiedades completamente nuevas sin ningún análogo clásico. Después de 2500 años los números primos se revelan no solo como los átomos de la aritmética sino como números cuánticos de un sistema hecho físicamente de  átomos. Si construyésemos el simulador podremos poner a prueba la existencia física de los números primos.

Las conclusiones están, asimismo, ligadas a la solución de uno de los mayores problemas de las matemáticas: La hipótesis de Riemann. La conexión proviene de la teoría analítica de  números que relaciona la función π(x) con los ceros no triviales de la función ζ(s) de Riemann. Según una famosa conjetura debida a Polya y a Hilbert: si la parte imaginaria de los ceros fueran autovalores de un sistema cuántico, la hipótesis quedaría probada. Empero, en este trabajo se ha encontrado que los primos son los números cuánticos del simulador, ello permite especular sobre la existencia de un sistema similar para los la función ζ(s).  Resolver el problema de la factorización por métodos de la física cuántica implicaría entonces, probablemente, verificar la validez  de la hipótesis de Riemann.

La investigación se ha desarrollado dentro del proyecto Quantum Information Technologies Madrid, QUITEMAD+ S2013/ICE2801.

[1] Quantum simulation of the integer factorization problem, Phys. Rev. A  97 032325 (2018) Jose Luis Rosales y Vicente Martín.

[2] Quantum simulation of the factorization problem, Phys. Rev. Lett. 117 200502 (2016) Jose Luis Rosales y Vicente Martín.